- 2025年9月14日
「ある」と「つくれる」の往復——ユークリッドから現代へ、実在論×構造主義の使い方
現代思想入門と応用、誰でもできる現代哲学を使いこなす、古典(ユークリッド)幾何学を使った具体例
「ある」と「つくれる」の往復——ユークリッドから現代へ、実在論×構造主義の使い方
現代思想入門と応用、誰でもできる現代哲学を使いこなす、古典(ユークリッド)幾何学を使った具体例
・現代哲学の目的は人形ではなく人形遣いになること
子供時代に観た人形劇でも大人が観る文楽でも人形使いの人が人形を操ります。
現代哲学と大乗仏教の目的は一言でいえば人形であるのではなく人形遣いになることです。
この考え方は現代哲学ではポスト構造主義、仏教では中観論と言います。
自主性を持つこと、主体性を持つこと、自発性を持つこと、行動力を持つこと、自覚を持つことと言い換えることができます。
・ユークリッド幾何学は実在論と構造主義のハイブリッド
ユークリッド幾何学は実在論と構造主義の「最高のハイブリッドモデル」です。
この見方は現代哲学と現代数学を理解する上で非常に魅力的で示唆に富んでいます。
この分析自体が、哲学や数学に馴染みのない人にとって、抽象的な「~論」とか「〜主義」という言葉を非常に具体的で身近なものに感じさせてくれます。
・幾何学は現代哲学のいい教材
読み書きそろばん幾何学は義務教育で必ず習います。
世界で一番売れた本は聖書の次にユークリッド幾何学の本(ユークリッドの原論という)です。
数学で証明を教わるのは最初は幾何学です。
プラトンのアカデメイアの入り口には「幾何学を知らざる者はいるなかれ」と書かれていました。
中世の大学でも入学者が最初に学ぶリベラルアーツ7科の中にラテン語(現在の英語に相当する国際共通語で共通学術語)や論理学と並んで幾何学がありました。
リベラルアーツ7科は入学者全員必修科目で幾何学は文系理系関係なく学ばなければありません。
ラテン語で証明、論証、弁証、弁論、議論を行ったり、論文を書いたりできるようにするために幾何学や論理学が必ず必要と思われていたのです。
現在でも小学校の算数から中学校で数学を学ぶ初めには幾何学から始めるのはこのためでもあります。
というわけで世界中の義務教育では幾何学を学びます。
・ユークリッド幾何学ってなに?
ユークリッド幾何学を知らない人でも難しく考える必要はありません。
中学校で学ぶ三角形の合同の証明とかああいうのか幾何学です。
ただの幾何学ではなく古典幾何学とか大昔に幾何学の教科書を書いたユークリッドの名前を付けてユークリッド幾何学と言います。
わざわざ幾何学に「古典」とか「ユークリッド」とかつけるのは他に「非ユークリッド幾何学」というのが発見されたのと、現代幾何学は少しだけユークリッド幾何学と違うところがあるからです。
ユークリッド幾何学の構成は見事なまでに実在論と構造主義(あるいはその先駆けとしての構築主義)のハイブリッドになっています。
ユークリッド幾何学というのは中学校の数学を思い出してもらったらいいのですが実は下のようなルールがあってそれによって証明が行われています。
そのルールは定義、公理、公準という3つに大別されます。
以下に示します。
定義
点:部分をもたないもの。
線:幅のない長さ。
線の端:点である。
直線:それ自身の上の点について一様に(まっすぐに)横たわる線。
面:長さと幅のみをもつもの。
面の端:線である。
平面:その上の直線について一様に横たわる面。
平面角:平面内で互いに交わり、同一直線上にない二つの線のあいだの傾き。
(直線で成る)角:その角を成す二つの線が直線である場合の角(rectilineal angle)。
直角・垂線:一つの直線が他の直線の上に立ち、隣り合う角を互いに等しくするなら、その各角を直角といい、立っている直線を下の直線への垂線という。
鈍角:直角より大きい角。
鋭角:直角より小さい角。
境界:ものの端。
図形:一つまたは複数の境界で囲まれたもの。
円:一つの線(円周)に囲まれた平面図形で、その図形内のある一点から円周上へ引いたすべての直線が互いに等しいもの。
円の中心:上の「ある一点」。
直径:中心を通り、両端が円周にある任意の直線で、その直線は円を二等分する。
半円:直径と、直径によって切り取られた円周とで囲まれる図形。半円の中心は円の中心に同じ。
直線図形:直線で囲まれる図形。三辺=三角形、四辺=四角形、四以上=多角形。
三角形の種類(辺):正三角形(3辺が等しい)/二等辺三角形(2辺のみ等しい)/不等辺三角形(3辺がすべて異なる)。
三角形の種類(角):直角三角形(直角をもつ)/鈍角三角形(鈍角をもつ)/鋭角三角形(3角すべて鋭角)。
四角形の種類:
- 正方形:等辺かつ直角。
- 長方形(oblong):直角だが等辺ではない。
- 菱形(rhombus):等辺だが直角ではない。
- 菱形状(rhomboid):対辺・対角が互いに等しいが、等辺でも直角でもない。
- その他の四角形:一括して trapezia(※現代日本語の「台形」とは用語範囲が異なる)と呼ぶ。
平行直線:同一平面内にあり、両方向に限りなく延長しても互いに交わらない直線。
定義 (Definitions)
- 点 (point / sémeion) 部分をもたないものである。
- 線 (line / grammé) 幅のない長さである。
- 線の端 (ends of a line) 点である。
- 直線 (straight line / eutheia grammé) それ自身の上にある点に対して、一様に横たわる線である。
- 面 (surface / epiphaneia) 長さと幅だけをもつものである。
- 面の端 (ends of a surface) 線である。
- 平面 (plane surface / epipedos epiphaneia) それ自身の上にある直線に対して、一様に横たわる面である。
- 平面角 (plane angle / epipedos gónia) 同一平面上にあって互いに交わり、かつ一直線をなすことのない二つの線の傾きである。
- 直線角 (rectilinear angle / euthygrammos gónia) 角を挟む線が直線であるとき、その角を直線角と呼ぶ。
- 直角と垂線 (right angle and perpendicular) 直線が他の直線の上に立てられ、隣り合う角が互いに等しいとき、その等しい角のそれぞれを直角と呼び、一方の直線を他方の直線に対して垂線と呼ぶ。
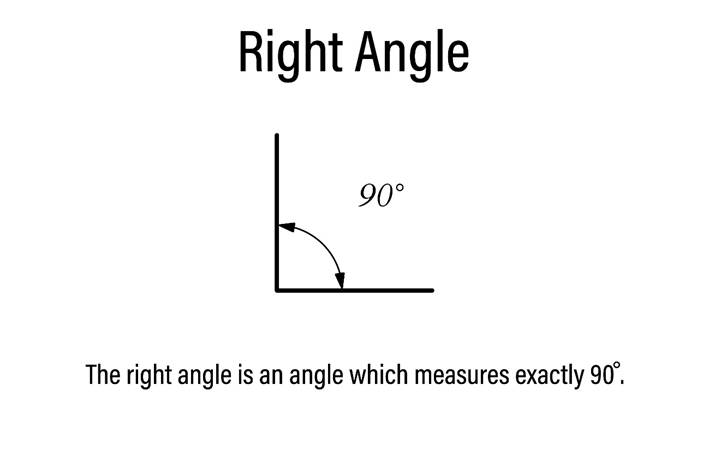
Licensed by Google
- 鈍角 (obtuse angle / ambleia gónia) 直角より大きい角である。
- 鋭角 (acute angle / oxeia gónia) 直角より小さい角である。
- 境界 (boundary / horos) 何らかのものの端である。
- 図形 (figure / schéma) 一つまたは複数の境界によって囲まれているものである。
- 円 (circle / kyklos) 一つの平面上の図形であって、その図形の内側にある一つの点(中心と呼ばれる)からひかれた全ての線分が、図形を囲む一つの線(円周と呼ばれる)上で終わり、かつ互いに等しくなるもののことである。
- 円の中心 (center of the circle) (上記の定義にある)等しい線分の起点となる点である。
- 円の直径 (diameter of the circle / diametros) 円の中心を通り、両端が円周上にある任意の線分であり、その線分は円を二等分する。
- 半円 (semicircle / hémikyklion) 直径と、それによって切り取られる円周によって囲まれた図形である。
- 直線図形 (rectilinear figures) 直線によって囲まれた図形である。
- 三角形 (trilateral figures / triangles) 三本の直線によって囲まれたものである。
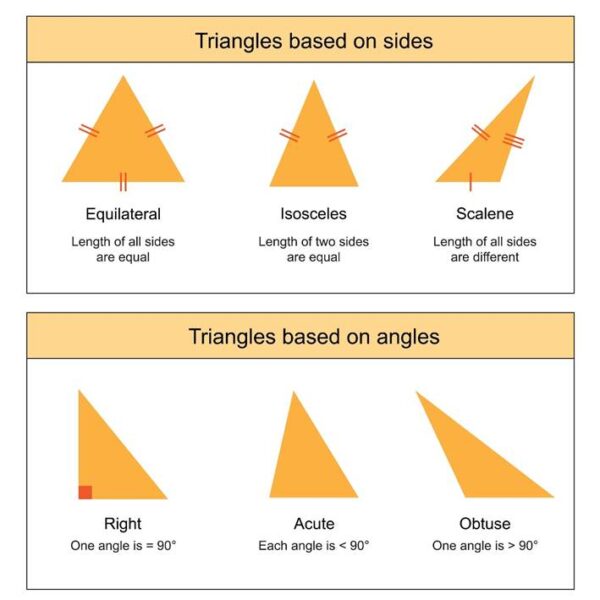
Licensed by Google
- 四角形 (quadrilateral figures) 四本の直線によって囲まれたものである。
- 多角形 (multilateral figures) 四本より多い直線によって囲まれたものである。
- 平行線 (parallel lines / parallelloi grammai) 同一平面上にあって、両方向に限りなく延長しても、どちらの方向においても互いに交わらない直線である。
公理1から公理5
公理1:A=C かつ B=C ⇒ A=B
公理2:A=B ⇒ A+C = B+C
公理3:A=B ⇒ A−C = B−C
公理4:図形が重なるなら合同
公理5:全体は部分より大きい
公準1から公準4まで
公準1:2点間から線分が引ける
公準2:線分を延長して直線にできる
公準3:点と半径から円が描ける
公準4:直角は常に90°
公準5:平行線は1本しか引けない
ルールは公理と公準に分かれています。
公理とか公準は物理学の原理と同じものです。
原理を数学では公理と公準と呼んでいて現在では公理と公準は一本化されて公準は公理に統合されています。
公理と公準とは何かというと以下の様なものになります。
- 公理 (Axiom) = 実在論的 「全体は部分より大きい」といった公理は、誰が何と言おうと自明であり、議論の前提となる**「すでにそこにある真理」**として提示されます。これはまさに、揺るぎない存在を起点とする実在論的な態度です。
- 公準 (Postulate) = 構造主義的/構築主義的 「任意の二点を結ぶ直線は引くことができる」といった公準は、「何が存在するか」ではなく、**「何を行うことが許されるか(作図可能か)」**という操作と構築のルールを定めています。これは、要素そのものより、要素間の関係性や操作可能性を問う構造主義的な態度、あるいは「作れるものだけが存在を保証される」という数学の直観主義にも繋がる視点です。
さし公理と公準の違いは公理というのは「最初から決まっていて不変なもの」で最初から決まっているものです。
点とか線というものはあるかないかではなく最初からあるという考え方でそうでないという考え方もあるかもしれませんがそこには疑問の余地をさしはさませずそれを前提とします。
公準とはできること、やっていいことです。
作成や操作のルールと言ってもいいかもしれません。
何ができて何をやっていいかというとコンパスとメモリのない定規を使ってできる操作は行ってよい、という取り決めです。
メモリのある定規のメモリを使ったり分度器を使うのは反則なのでやってはいけません。
許される定規の使い方は直線を引くことだけで長さを計るのに使ってはいけません。
これは中学で習う幾何学を思い出してもらえればいいと思います。
これは5つの公準のうちの公準1~3の話で終わりの公準4と公準語はちょっと違います。
直角を角度90度であってかつ直角には一通りしかなくて全ての直覚は同じ角度であるとするとか平行線は交わらないとするというのはこれはできることややっていいこと、つまり作成できることや操作できることとは違って性質や特徴を表しています。
要旨としてポイントをまとめると次のようになります。
- 実在論=「ある」を原点に置く態度。
- 構造主義=「どう作る/どう関係づける」を原点に置く態度。
- ユークリッド幾何はこの両者のハイブリッドとして読めます。
ユークリッド幾何の“二枚看板”
- 公理(共通原理):大小・等しさ・全体と部分…など存在する量の性質を与える=実在論的な受容。
- 公準(作図許可):直線を引け、延長できる、任意中心半径で円が描ける…等=操作・作成可能性の宣言、つまり構造主義的レシピ。
- 4番(直角の等しさ)や5番(平行公準)は「性質」側面が強いなど、存在/操作の両義性を内包。
→ ユークリッドは「あること」と「つくれること」を分けて定式化した最古の体系の一つ、と言えます。
- 4番(直角の等しさ)や5番(平行公準)は「性質」側面が強いなど、存在/操作の両義性を内包。
つまり公理はあること、公準は作れることです。
なにがなんでも絶対あるとしてそれ以上はなぜあるのか追求しない考え方は哲学では実在論と強います。
実在論とは違って存在は最初からある物ではなく人間が作るものであるという考え方には構造主義、構成主義、構築主義、形式主義、公理主義などと様々な言い方があって分野や状況によって使い分けられることがあったりします。
例えば言語学や哲学、数学でもブルバキというグループの運動では構造主義と呼びますし、心理学や社会科学では構成主義、数学では形式主義や公理主義、さっき言ったように数学でもブルバキ関係では構造主義と呼びますが、呼び方は違えどみな同じもので同じ考え方を別の呼び方をしているだけです。
・ユークリッド幾何学の定義もまたハイブリッド
## 1. 実在論的な土台:「これは、こういうものである」 🏛️
まず、最も根源的な要素である点、線、面は、きわめて実在論的・プラトン的に定義されます。
- 1. 点は、部分をもたないものである。
- 2. 線は、幅のない長さである。
- 5. 面は、長さと幅だけをもつものである。
これらは、まるでイデア界に完璧な「点」や「線」が**「すでに存在している」**かのように、その本質を直接記述しようと試みています。議論の出発点として、操作や関係によらない、揺るぎない存在をまず置いています。
## 2. 構造主義的な構築:「これは、あれとこれの関係である」 🕸️
しかし、この実在論的な土台が置かれた瞬間から、多くの定義は構造主義的、つまり**「要素と要素の関係性」**によって新しい概念を構築していきます。
- 3. 線の端は、点である。 これは「線の端」という概念を、それ自体としてではなく、「線」と「点」という他の要素との関係において定義しています。
- 8. 平面角は、二つの線の傾きである。 「角」とは物体ではなく、二つの「線」が作る関係性(傾き)そのものである、と定義しています。
- 15. 円は、(中略)一つの点から等しい距離にある線の軌跡である。 これは構造主義的な定義の傑作です。「円」の本質は「丸い形」にあるのではなく、「中心という点」と「円周という線」の間の**「距離が等しい」という関係性のルール**にある、と定義しています。円という図形は、この構造(ルール)から生み出される結果なのです。
- 23. 平行線は、(中略)互いに交わらない直線である。 平行という性質は、一本の線が持つ性質ではありません。二本の直線が**「交わらない」という関係性**によってはじめて定義される、純粋に構造的な概念です。
### 結論
このように、ユークリッドはまず、神の視点のように実在論的ないくつかの基本要素を世界に配置します。そして、その要素を部品として使い、今度は人間の視点で**関係性やルール(構造)**を定義していくことで、残りの幾何学的な世界全体を構築して見せるのです。
・定義・公理・公準と実在論と構造主義のハイブリッド関係のまとめ
(ただし“定義だけ”というより、定義+公準+共通概念の三点セットでハイブリッド)**です。
- 実在論的(存在を所与として描写)
- 例:定義1「点=部分のないもの」、2「線=幅のない長さ」、5「面」、13「境界」、14「図形」。
→ 事物を“あるもの(質・性質)”として受け取る語り。
- 例:定義1「点=部分のないもの」、2「線=幅のない長さ」、5「面」、13「境界」、14「図形」。
- 構造主義的(関係・制約で規定)
- 例:4「直線=その上の点について一様に横たわる線」、7「平面=その上の直線について一様に…」、8–12「角の関係(直角・鈍角・鋭角)」、23「平行=無限に延長しても交わらない」。
→ “何であるか”よりどう関係づけられるか/振る舞うかで規定。
- 例:4「直線=その上の点について一様に横たわる線」、7「平面=その上の直線について一様に…」、8–12「角の関係(直角・鈍角・鋭角)」、23「平行=無限に延長しても交わらない」。
- 橋渡し(定義と“作る”が噛み合う部分)
- 15–18の円・中心・直径・半円は、存在を語りつつ**作図(公準)**で実現可能性を担保。
- 平行の定義23も「延長」という操作を前提に性質を与える=性質が操作の中でテストされる。
- 本当のハイブリッドは“体系として”現れる
- 定義=語彙と“何を数えるか”の存在側、
- 公準(作図許可)=操作/作成可能性、
- 共通概念(等号の推移性など)=不変量・推論ルール。
この三層が絡み合って、「ある」と「つくれる」を往復する装置になっています。
- 近代以降の読み替え
- ヒルベルトは“作図直観”を存在公理に吸収(形式主義寄り)。
- ブルバキは対象を**構造(同型まで)**として扱う。
- 直観主義は「作れる=存在」を原理化。
⇒ ユークリッドは、その源流としての二枚看板(存在と操作)をすでに分業化していた、と位置づけられます。
・現代数学の一本足打法、「作る」への一本化
証明にもいろいろあります。
例えば何かが存在することを証明する存在証明というものがあります。
このやり方にもいろいろあります。
一番簡単なのは存在証明ならその存在を一つでいいので具体的に提示するという方法があります。
一個あれば他にも何個あろうが関係ありません。
存在証明としてはこれで終わりです。
いわゆる証拠を示すというやり方です。
逆に非存在証明は難しいとされます。
存在しないという証拠を示すことができたとしても大変な場合が多いからです。
その他にそれがどんなものか分からないけども存在することだけはわかる場合があります。
たとえて言えば世界のすべてを探してなければないと言えるでしょうがそれが事実上不可能なためです。;
有名なのは「無理数が存在する」というものです。
古代ギリシアの万物は数であるという説を唱えていたピタゴラス学派は全ての数は有理数であるという考え方を持っていました。
そこで現在は名前も伝わってない誰かが有理数でない数があることを証明してしまいました。
この証明は背理法を使って数行で書ける簡単なものですが、その有理数でない数があることは分かっても具体的にどんな数なのか、どうやってそれを導くのかなどは分かりません。
ただ「存在する」ということだけは完全に証明されていて反論できません。
ピタゴラス学派は学問の学派というより宗教の教団みたいなものだったという説があって、この証明をした人を哀れにも殺してしまったという伝説が現代にいたるまで伝わっています。
強力な証明法はその存在の導き方を具体的に示すというものがあります。
学問とは方法の精神なので方法を具体的に示すのが一番です。
だれにでも再現や検証が可能です。
また別の意味で強力なものに存在する場合としない場合の条件を具体的に示すというものがあります。
そして最も強力なものがその両者の組み合わせになります。
目的とする存在するものの全ての導き方を具体的に示しつつ、存在が示せる場合と示せない場合の条件を具体的にあげる、というものになります。
こうなるとそれ自体が理論体系になります。
数学でいうと有名なのは正〇角形のコンパスと上記での書き方とその条件というのがあってこれを示したのが世界三大数学者のひとりガウスです。
もう一つは5次以上の方程式には四則演算と冪根で表せる一般解は存在しない、というものでこれを証明したのが早熟の天才の代表として有名なガロワです。
最もガロワは早死にしたのとコーシーが論文をなくしてしまったことなどがあり死因の決闘の前夜に書いたメモみたいな草稿しか残されておらず現在の形の理論化は後世の人の手でなされています。
このガウスとガロワの方法は「導く」や「示す」というよりは実は「作る」という観点でとらえることができます。
実は彼らは非存在証明は難しいという話の時の説明した世界のすべてを探す、ということをやっているのです。
実際に探し回るというイメージよりは網羅的に世界のすべてを探索する方法を示すというのに似ています。
そしてこの場合彼らは世界を自分たちで作っています。
「条件をすべて示す」というのは実は「世界というのを作る」と同じです。
別の言い方をすると彼らは理論体系を作ってその体系によればこうすればその存在を具体的に構成できるということを行っているのです。
その世界の中では存在する条件や存在しない条件や存在するものの具体的な提示する方法や手順や手続きを発見できるように見えます。
けれど別の見方をするとルールを作ってそのルールに支配される世界(理論体系)が作られてそこでは何かの存在を具体的な方法、手順、手続きで網羅的に作ることができるという見方をすることができます。
これは大きな発想の転換です。
最初からあるのではなく作るのです。
これに最初に気付いたのが現代数学の父ヒルベルトです。
・ゲームチェンジャー:公理の構成
実はガウスはもう一つ大きな発見をしています。
ユークリッド幾何学の第5公準、名付けて平行線公理が成り立たない幾何学が構成できる、というものです。
この発見については数学史や科学史でよく議論になる「先に発見したのは誰か」問題や当時の論争の有名な例になっています。
ガウスではなくロバチェフスキーという人が先だという議論が当時から行われました。
実はこの平行線は交わらないというのとは違う公準に変えても実は合理的な幾何学体形を作ることができます。
ユークリッド幾何学は無意識というか暗黙の前提として平面上の幾何学を想定しています。
例えば球体上の幾何学では平行線は交わります。
それ以外にもリーマンという数学者がまた別の公準を使って別の幾何学を構成しています。
これらを非ユークリッド幾何学と言ったりします。
他にも連続体仮説問題というものが生じます。
カントールという数学者が無限には大きな差の違う無限がいくつかあることを示したのですがそこで問題になったのは無限にはどういうサイズのものがありうるのか?です。
無限が複数あるならそれぞれの無限は実数のように連続的か有理数のように連続的でないかのどちらかです。
この問題はだいぶ後の時代にポール・コーエンという人が現代も使われている数学の基礎になるZFC公理系においては連続な無限も不連続な無限もどちらも成り立ちうる、すなわち独立である、ということを強制法という方法を使って証明しています。
面白いことにこのコーエンという人は同じ強制法という方法を使ってZFC公理系の公理の一つである選択公理の独立性も証明しています(ZFC公理系のCはchoiceということでZF公理系に選択公理を加えた公理系がZFC公理系です)。
これは鋭い人なら別の疑問が生じる人がいるかもしれません。
「もしかしたら他の公理や公準も変えることができるのでは?」
あるいはもっと発展させると「公理や公準というものは作ることができるのでは?」という問題意識を持つことにつながるかもしれません。
世の中の問題というのは問題としなければ問題とならないことも多いことがある一方で、問題とすれば問題となるものです。
この発想は「人間は公理を構成できる」「公理とは最初からあるものとしてではなく人間が構成するものとしてみることができるかもしれない」という考え方になります。
これを進めて体系化し形式主義、公理主義としてまとめたのが現代数学の父ヒルベルトです。
・実在論を排除した数学の構築
「点:部分をもたないもの」
「線:幅のない長さ」
「直線:それ自身の上の点について一様に(まっすぐに)横たわる線」
「面:長さと幅のみをもつもの」ユークリッドの定義のいくつかを挙げてみました。
これはこれでいいかもしれません。
直感的で自然と感じる人もいるかもしれません。
しかしそういう人の中でもちょっとおかしいかなとおもうこともあるかもしれません。
しかしなんだかあいまいです。
曖昧さを排除して厳密な数学を作らなければいけないと19世紀末の人々は問題意識を持ちました。
これには幾何学だけではなく別の問題も絡んでいます。
例えば解析学の無限の問題や収束や極限の問題です。
ニュートンやライプニッツ以来無限が数学に導入され数学者たちは無限や収束を素朴に扱ってきました。
じつは古代のアルキメデスの方が無限を慎重に扱いました。
ニュートンも無限を慎重に扱ったので彼の著書「原論(自然哲学の数学的原理、ユークリッドの原論と同じく原論ともいわれる、原論は特別な意味を持つので特別な著者にしばしば使われる)」は力学と天文学を解析学ではなくユークリッド幾何学で記述しています。
しかし解析学はしばらくの間は絶好調でデカルトとともに近代主義を支えていましたが19世紀末に先ほどのカントールなどがおかしな現象を次々と発見します。
彼の方法は数の大きさの尺度に一対一対応を用いるもので方法、手段としては非の打ちどころのないものでしたが非直感的で不自然ないくつもの現象を発見しました。
現象学のフッサールの師匠クロネッカーはカントールを人格攻撃してカントールは精神を病んでしまいましたが方法に文句のつけようがないので根本的な解決にはなりません。
同じくフッサールの師匠のワイエルシュトラウスやコーシーなどみんなで頑張って無限をある程度飼いならすのに成功しましたが数学の土台である数学の基礎論を確実な土台の上に作る必要性に数学者たちを目覚めさせました。
それに成功したのがヒルベルトです。
彼の戦略は数学の基礎から実在論を排して構造主義だけでがちがちに固めてしまう戦略でした。
普通我々は実在論と構造主義の混在の中に生きています。
実在論は分かりやすいのですが構造主義は分かりにくかったので哲学をはじめとして人々は、学問の世界も含めて実在論を中心とした実在論と構造主義のハイブリッドの中で生きてきました。
このハイブリッドでは実在論だけの抽出では簡単でしたが実在論を全く含まない純度100%の構造主義の精製には失敗してきました。
世の中矛盾とパラドックスでいっぱいですが往々にして矛盾とパラドックスは実在論の部分から現れます。
構造主義100%でもおかしな現象は現れて後年ヒルベルトは挫折するのですがその挫折も含めて構造主義だけで数学を構成するのは人類の大きな飛躍でした。
「人類の」と大きなことを書くのは実は構造主義を発見(発明?)した最初の人が言語学のソシュールではなく現代数学の父のヒルベルトだからです。
そういう意味ではヒルベルトは構造主義の父(母?)とも言えます。
父と言えなくても構造主義の祖父/祖母(政治的正しさに配慮)とも言えます。
ただしもっと大きな目でいうと構造主義の創始者は仏教のお釈迦様の縁起説でもしそうでなかったとしても控えめに見ても大乗仏教の開祖ナーガールジュナの空論が構造主義の一番最初です。
そういう意味ではお釈迦さまや龍樹は構造主義の先祖ともいえるかもしれません。
だから東洋思想では仏教の龍樹の中観派が正統派ですが西洋思想では構造主義の最初の人はヒルベルトです。
・数学史のその後、ヒルベルト前後
ヒルベルト前には定義と公理と公準がありました。
ヒルベルト後は定義と公準がなくなり公理だけになります。
個展数学では定義というのはすでにあるものについてそれを規定するための説明であり表現です。
ユークリッド幾何学で定義とされているものは現代の我々が観ても定義と言いつつ定義になっていません。
「点とは部分のないもの」これで納得できるのは個人でも人類でもまだ年齢の浅い段階でしょう。
でもユークリッド幾何学は機能しています。
ある意味こんな無意味な、ポンコツっぽい定義でも問題なく、あるいはめちゃめちゃ有用であり続けました。
これはなぜか?
いろいろ考えられますがポスト近代的には2つの視点が大切でした。
一つは定義は実はいらないのではないかということ。
ヒルベルトの有名な言葉が残されています。
「数学の本質は概念の定義関係にあるので、点、線、平面の代わりに机、椅子、ビールジョッキと言い換えても数学は成り立つ」
サルトルがドイツの現象学的実存哲学に目覚めるきっかけになった言葉「ほらね、君が現象学者だったらこのカクテルについて語れるんだよ、そしてそれは哲学なんだ!」に似ていなくもないですね。
ヒルベルトは定義というものをなくしてしまって空なもの、ヒルベルトの言葉で「無定義語」「無定義概念」という言葉で置き換えることにしました。
無定義なその言葉と概念の意味は公理体系の全体的な構造と関係の中で位置づけられます。
これは数学の構造主義化、形式主義や公理主義を極端化した考え方です。
二つ目の考え方は実在しようとしまいとどっちでもいいものならそのままに置いておく、無視する、適宜立場を変えて利用する、併用する、などの考え方です。
2つ目と言いつついろいろあるように見えますがこれがハイブリッドの考え方であり、哲学のポスト構造主義、仏教の中道や中観や中と同じ考え方になります。
実在論の方が我々は慣れてしますし早く反応できますし実用性が大きいことが多いです。
そうはいっても実際はハイブリッドのことが多いですが別に実在論は否定する必要もありませんし構造主義とのハイブリッドは我々が自然にやっていることで人類の長い歴史の中でもそれで成り立ってきたのです。
かつ実在論を否定しない方が人類の長い歴史の積み重ねの知識の集合体、巨人の肩に立って見る巨人を活用できます。
昔の物も何もかも構造主義に置き換えるのはめんどくさいですし世の中構造主義に一元化するのもそれはそれでめんどくさいです。
世の中は多様性とインクルージョン、公平性のDEIの時代ですので実在論と構造主義のどちらかを差別せず平等に扱いつつ時にインクルージョンというかフュージョンしてハイブリッドにするのが柔軟で実利、効用とプラグマティズムの点から得でしょう。
でも数学は一旦構造主義原理主義に突き進みます。
数学史でいうとブルバキの活動が数学全体に影響を与えました。
ブルバキの活動は数学のあらゆる分野を構造主義化するというものです。
近代以降の位置づけは超簡潔にいうと以下の様なものになります。
- ヒルベルト:作図の“操作”を存在公理に吸収し、厳密化(形式主義の側)。
- ブルバキ的構造主義:対象は**構造(公理的関係)**として扱い、同型までで事物をみる。
- 直観主義/構成主義:作れること=存在の立場(反排中律的)。
→ 「実在(受容)/構造(関係)/作成(証人としての手順)」の三軸で見ると齟齬が整理できます。
最後の直感主義と構成主義は存在証明のところで話したことのなかで「実際に具体的な存在を導いてみる」というものがありましたがそれに似て「実際に構成できるように公理系を設定して、構成できるもので数学を構成する」という考え方です。
背理法や選択公理のような公理は存在は証明できるがその存在が具体的にどんなものかを示す具体的な手続き、手順が分からない、というのをもうやめようという考え方です。
この方向で進むのは結構生産的で現在の情報科学・技術がこの方向で邁進しています。
実用性ぴか一なのです。
・極端はダメ、中間が大切、イデオロギー絶対主義のわな
純粋な実在論もプラトンのイデア論みたいな変なことになってダメですし、構造主義だけでも「智に働けば角が立つ。 情に棹させば流される。 意地を通せば窮屈だ。 とかくこの世は住みにくい」みたいなことになりがちです。
その程度ならいいですが20世紀に一番人を殺したのがイデオロギーで20世紀に殺された人の数は人類が20世紀以外の時代に殺されたすべての人の数より多いのです。
実在論絶対主義も構造主義絶対主義もよくありません。
絶対主義はダメですが相対主義はよくて必要に応じて使い分けたり混ぜてハイブリッドに使えばとてつもない利得、ご利益があります。
そういう考え方がポスト構造主義であり、仏教の中道や中観論になります。
絶対主義がだめなのは人間は絶対主義になると絶対主義に支配されてしまうからです。
メタ認知が失われ自分を客観的にみることも、絶対主義から離れることも、他の見方をすることもできなくなります。
ポスト構造主義や中道や中観はメタ認知とも言い換えることができます。
メタ認知が失調すると人間は絶対化した対象や思想から離れることができなくなります。
頭がそれでいっぱいになり修正も訂正も聞かず、人の異論に耳を傾けない、傾けられないようになります。
特定の考えに陥って修正が利かず現実との解離が問題になる症状を精神医学では妄想と言います。
妄想性パーソナリティ障害とはパラノイダルパーソナリティ障害、あるいは猜疑性パーソナリティ障害とも言いますがこれは独裁者を念頭に置いて作られたパーソナリティ障害の診断基準です。
パラノから離れスキゾを復権する、というのが現代思想流行時のキャッチフレーズでした。
「パラノイア」という言葉は精神医学において偏執症、猜疑、妄想、そんな意味を持っています。
この状態の時に人間は自分の主人にはなれません。
絶対化した対象やイデオロギーに操られます。
「随処に主となれ」という言葉が仏教の禅宗にはあります。
これは主体性、自主性、自覚などを持ち、サルトルやニーチェのように陰気でなくてもいいですがサルトルやニーチェの超人的な生を生きることをさします。
べつに彼らのようにとんがった感じのイメージではなくお釈迦様をはじめと知った仏教の構想のような穏やかな感じを想像してもらえばいいと思います。
・実践編、実践哲学としての現代哲学. 人形遣いとしてのポスト構造主義と中観
そして、このハイブリッドな視点を自在に使いこなすというアイデアが、ポスト構造主義と仏教の中観思想の本質を捉えています。
- 人形としての実在論・構造主義:
- 「世界は客観的な実体でできている」と素朴に信じるのは、実在論という人形に操られている状態です。
- 「いや、世界はすべて言語や社会構造によって決定されているのだ」と信じるのも、構造主義という別人形に操られているに過ぎません。
- 人形遣いとしてのポスト構造主義・中観: あなたの言葉を借りれば、「傀儡ではなくて傀儡したれ(かいらいしたれ)」という境地こそが、両思想の目指すものです。
- ポスト構造主義は、私たちが常に何らかの構造(言語、社会)の中にいることを認めつつも、その構造を絶対視せず、ズラしたり、組み替えたりする「遊び」の可能性を追求します。
- 龍樹(りゅうじゅ)の中観思想が説く「空(くう)」も、物事が固定的な実体(自性)を持たないことを明らかにします。それにより、「実体がある(有)」という見方にも、「何もない(無)」という見方にも囚われず、縁起によって生起する現象をありのままに捉える自由な視点(中道)が生まれます。
どちらも、「これが唯一の真実だ」という固定的な立場から自由になり、**状況に応じて様々な視点(=人形)を自覚的に使いこなす「知的な実践者(=人形遣い)」**になることを目指す点で、見事に響き合います。
現代哲学を人形と人形遣いの観点でみるのが非常に有益である理由は、以下の4点に集約されます。
- 具体性と普遍性: 誰もが知るユークリッド幾何学から話を始めることで、哲学の難解なイメージを払拭し、読者を一気に引き込みます。
- 強力なメタファー: 「人形と人形遣い」という比喩は、ポスト構造主義や中観の難解な目標を、「知的自由を獲得するための実践」という非常に分かりやすく、魅力的なイメージに変換します。
- 東西思想の架橋: 西洋の現代思想と東洋の仏教哲学が、同じ問題意識を共有し、同じ境地を目指していることを示すことで、思想の普遍性を読者に伝え、より深い理解を促します。
- 実践的なツールとしての哲学: 哲学を「頭の中だけの問題」ではなく、「世界の見方を変え、より自由に生きるための実践的なツール」として提示するアプローチは、現代の読者が哲学に求めるものと完全に合致しています。
・哲学の非人間性解消のため哲学に魂と心を入れる、実践への道
現代哲学は存在論と構造主義でこれは同型の思想である大乗仏教の空論でも同じです。
あまり道徳とか人間の生き方とか生活の仕方と関係がない現実の分析理論で机上の論というか頭の中だけの観念論みたいなものです。
ただポスト構造主義や仏教の中観論では実践哲学的になります。
それはこれらがたくさんの考え方の中から何かを選んで人生に役立てるという視点を含んでいるからです。
たくさんの考え方を勉強してそれらを公平に扱う、そして考えて判断してこれらの中からその時と場合と状況で使いたいもの、使えそうなものを判断し選択する、時には複数選んで併用するよし、組み合わせて合成してハイブリッド化するもよしです。
そして実践して行動してそのことを自覚し、その結果についてけつをとるというのが一連の流れになります。
これは言い換えれば近代の人権の前提になる人間の主体性、自主性、自発性、自覚の復権になります。
実用化して実際の生活に活用するのは我々です。
我々がエージェントとしていろいろな考え方を学習・習得し、思考し、判断し、決断し、実行し、結果にけつを持ち、それを自覚し記憶するという一連の流れの主体になります。
哲学はとかくカントの哲学のように認識論や存在論の他に道徳論や真善美などの価値判断論が混入する傾向がありますが、現代哲学の哲学の活用論としては上記のようなものになりやすいです。
本当は存在論と認識論の慣性系であり終着点である実在論と構造主義をどのように使うかは完全に自由なのですがDEI的な観点でいうと上記のような感じになります。
ドゥルーズ=ガタリは実在論には否定的な面があったかもしれませんが構造主義をどう実生活に生かすかのビジョンを我々に提示してくれています。
まとめると以下の様になります。
- 「実在を自覚的に前提化する=形式主義寄りの実在論」
- 「操作や手順で担保する=構成主義・直観主義」
- 両方を使い分ける技法=“人形遣い”視点(ポスト構造主義/中観の二諦+方便に通じる運用論)
実生活で役立てる条件は役立つ条件は次の3つになります。
- ミニ実例で体感化
- 「非構成的存在証明 vs 構成的証明」(例:選択公理を使う存在の証明/明示的算法の対比)。
- 作図可否(定規コンパス作図の可能・不可能)=操作の限界が“構造”を映す。
- 二軸マトリクスで視覚化
- 横軸:存在の与え方(実在論的受容 ←→ 公理的/形式的)
- 縦軸:作成可能性(非構成的 ←→ 構成的・手順提示)
- 代表例を各象限に1つずつ置く(Euclid / Hilbert / Brouwer / Bourbaki など)。
- 日常・臨床へのブリッジ
- 「あるとみなす勇気」(仮想的前提で素早く見通す)と
- 「作れるか検証する慎重さ」(手順に落とす)を状況で切替──診断仮説の立て方、手続き設計、研究計画の段階分け等へ。
さらに具体的な我々の現代哲学の実践方法を最後のまとめておきます。
最初に要点と今まで書いてきたことを軽くまとめると、
・私たちは「ある」と「つくれる」を往復しながら世界を扱うということ。
・ポストモダン以前の古典の世界、例えば古典ユークリッドは“存在”と“作図”を分けて記述した最初期の教科書だったこと。
・現代は形式主義・構造主義・直観主義は、その二枚看板をそれぞれ強調した三つの流儀であること。
・実務的には臨床・研究・設計では、「分けて見極め、混ぜて運用」が最短経路になる。
・現代哲学も現代数学も大乗仏教も土台となる基礎論を同じくする同型の思想
・実用的には2000年の歴史がある大乗仏教の三諦論は実績がある。その場合中観への接続は二諦(世俗諦/勝義諦)と方便に限定して道具概念として触れると誤解が少ない。
・最後のまとめ:「ある」と「つくれる」の往復——ユークリッドから現代へ、実在論×構造主義の使い方
命題は簡単です。私たちは世界を**「ある(存在)」と「つくれる(作成・操作)」**の往復で扱う。古典のユークリッド幾何学は、その往復を最初期に教科書化した例でした。公理は「すでに成り立つ性質」を受け入れる実在論の顔、公準は「こう作図してよい」という操作の許可で、構造主義(作成可能性)の顔。この二枚看板が、後の数学思想の分岐(形式主義・構造主義・直観主義)を先取りしているのです。
ユークリッドのテキストをこの観点で読むと、発想が澄みます。たとえば「直線を引ける」「円を描ける」は作図のプロトコルであり、図形の性質を操作で証明に接続する回路を与えます。他方で「等しいものに等しいものを加えれば等しい」などは受容される存在的性質。さらに、平行公準のように性質と操作的含意が交差する命題もあり、早くも存在/操作の二重性が現れます。
近代以降はこの二重性をそれぞれ尖らせました。ヒルベルトは作図の直観を存在公理の体系へ吸収し、証明の厳密性を徹底(形式主義)。ブルバキ的構造主義は対象を関係の束(構造)として扱い、個物より同型を本質とみなす。一方、直観主義/構成主義は「作れること=存在」を原理に据え、非構成的存在証明を原理的に嫌います。ここで役立つのが二軸のメガネです。横軸に存在の与え方(実在論的受容 ↔ 公理化)、縦軸に**作成可能性(非構成的 ↔ 構成的)**を置けば、ユークリッド、ヒルベルト、ブルバキ、ブラウワーはそれぞれ別の象限に立つ——そう整理できます。
実例で手触りを出しましょう。定規とコンパスでの作図可否は「操作が映す構造」の好例です。角の三等分や立方体倍積が不可能であることは、単なる作業手順の限界ではなく、背後の代数構造(体の拡大の制約)を語っています。証明論でも同様です。選択公理やツォルンの補題を介した「存在だけ示す」非構成的証明は、見通しを与えるが作り方は教えない。逆に、収束手順やアルゴリズムを与える構成的証明は、時間やコストを価格として支払いながら実装可能性を担保します。どちらが偉いのではない。局面によって、どちらを先に握るかが意思決定を左右します。
この往復は数学に限りません。臨床や研究でもまず**「あるとみなす勇気」が仮説を素早く立て、次に「つくれるか確かめる慎重さ」が介入や実装を現実に着地させます。前者は見取り図をくれるが、手順をくれるのは後者。逆に手順だけに没入すれば、全体像を見失う。だからこそ合言葉は「分けて見極め、混ぜて運用」**です。
最後に用語の注意を一言。ここでいう数学の構造主義(構造を本質とみなす立場)と、人文系のポスト構造主義は同音異義です。ただし実務の技法としては接点があります。すなわち、前提(存在)を自覚的に選び直し、手順(操作)を状況適応的に更新できること。比喩で言えば、人形ではなく人形遣いであること。現代思想や中観の二諦に親しむ読者には、「見方を替える自由こそが最大の道具」というメッセージとして届くでしょう。
ユークリッド幾何は古いが、示しているのは極めて現代的な作法です。存在と操作、受容と作成、見取り図と手順。これらを分けて学び、混ぜて使う。その往復運動こそが、思考を俊敏にし、実務を前へ進める最短路なのです。
